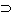 q", "p" und
"q" in der Form
"(p
q", "p" und
"q" in der Form
"(p 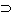 q) . (p) :
q) . (p) :
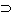 : (q)" miteinander verbunden eine
Tautologie ergeben, zeigt, daß q aus p und
p
: (q)" miteinander verbunden eine
Tautologie ergeben, zeigt, daß q aus p und
p 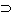 q folgt.
q folgt.
Daß "(x) . fx :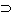 : fa" eine Tautologie
ist, daß fa aus (x) . fx folgt, etc. etc.
: fa" eine Tautologie
ist, daß fa aus (x) . fx folgt, etc. etc.
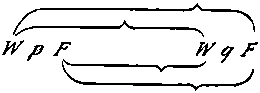
und die Zuordnung der Wahr- und Falschheit des ganzen Satzes und der Wahrheitskombinationen der Wahrheitsargumente durch Striche auf folgende Weise:
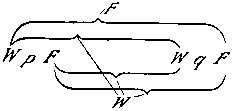
Dies Zeichen würde also z.B. den Satz
p 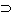 q darstellen. Nun will ich z.B. den
Satz ~(p . ~p) (Gesetz des Widerspruchs) daraufhin
untersuchen, ob er eine Tautologie ist. Die Form
"~
q darstellen. Nun will ich z.B. den
Satz ~(p . ~p) (Gesetz des Widerspruchs) daraufhin
untersuchen, ob er eine Tautologie ist. Die Form
"~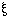 " wird in unserer Notation
" wird in unserer Notation
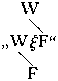
geschrieben; die Form "
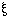 .
. 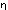 " so:
" so:
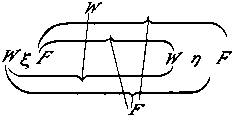
Daher lautet der Satz ~(p . ~q) so:
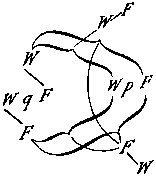
Setzen wir hier statt "q" "p" ein und untersuchen die Verbindung der äußersten W und F mit den innersten, so ergibt sich, daß die Wahrheit des ganzen Satzes allen Wahrheitskombinationen seines Argumentes, seine Falschheit keiner der Wahrheitskombinationen zugeordnet ist.