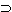HOME TOP UP PREV NEXT 1 2 3 GERMAN MAP      Tractatus Logico-Philosophicus 6.120

6.120

6.1201

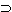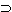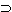That e.g. the propositions "p" and "~p" in the connexion "~p . ~p" give a tautology shows that they contradict one another. That the propositions "p  q", "p" and "q" connected together in the form "(p  q) . (p) :: (q)" give a tautology shows that q follows from p and p  q.

That "(x) . fx :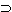: fa" is a tautology shows that fa follows from (x) . fx, etc. etc.

6.1202

It is clear that we could have used for this purpose contradictions instead of tautologies.

6.1203

In order to recognize a tautology as such, we can, in cases in which no sign of generality occurs in the tautology, make use of the following intuitive method: I write instead of "p", "q", "r, etc., "TpF", "TqF", "TrF", etc. The truth-combinations I express by brackets, e.g.:

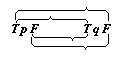
and the co-ordination of the truth or falsity of the whole proposition with the truth-combinations of the truth-arguments by lines in the following way:

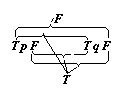
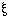This sign, for example, would therefore present the proposition p  q. Now I will proceed to inquire whether such a proposition as ~(p . ~p) (The Law of Contradiction) is a tautology. The form "~" is written in our notation

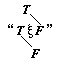
the form " 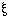. 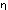" thus :--

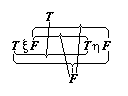
Hence the proposition ~(p . ~q) runs thus :--

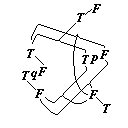
If here we put "p" instead of "q" and examine the combination of the outermost T and F with the innermost, it is seen that the truth of the whole proposition is co-ordinated with all the truth-combinations of its argument, its falsity with none of the truth-combinations.