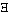HOME TOP UP PREV NEXT 1 2 3 4 ENGLISH MAP      Logisch-philosophische Abhandlung 5.45

5.45

Gibt es logische Urzeichen, so muß eine richtige Logik ihre Stellung zueinander klar machen und ihr Dasein rechtfertigen. Der Bau der Logik aus ihren Urzeichen muß klar werden.

5.451

Hat die Logik Grundbegriffe, so müssen sie von einander unabhängig sein. Ist ein Grundbegriff eingeführt, so muß er in allen Verbindungen eingeführt sein, worin er überhaupt vorkommt. Man kann ihn also nicht zuerst für eine Verbindung, dann noch einmal für eine andere einführen. Z.B.: Ist die Verneinung eingeführt, so müssen wir sie jetzt in Sätzen von der Form "~p" ebenso verstehen, wie in Sätzen wie "~(p v q)", "(x) . ~fx" u.a. Wir dürfen sie nicht erst für die eine Klasse von Fällen, dann für die andere einführen, denn es bliebe dann zweifelhaft, ob ihre Bedeutung in beiden Fällen die gleiche wäre und es wäre kein Grund vorhanden, in beiden Fällen dieselbe Art der Zeichenverbindung zu benützen.

(Kurz, für die Einführung der Urzeichen gilt, mutatis mutandis, dasselbe, was Frege ("Grundgesetze der Arithmetik") für die Einführung von Zeichen durch Definitionen gesagt hat.)

5.452

Die Einführung eines neuen Behelfes in den Symbolismus der Logik muß immer ein folgenschweres Ereignis sein. Kein neuer Behelf darf in die Logik -- sozusagen, mit ganz unschuldiger Miene -- in Klammern oder unter dem Striche eingeführt werden.

(So kommen in den "Principia Mathematica" von Russell und Whitehead Definitionen und Grundgesetze in Worten vor. Warum hier plötzlich Worte? Dies bedürfte einer Rechtfertigung. Sie fehlt und muß fehlen, da das Vorgehen tatsächlich unerlaubt ist.)

Hat sich aber die Einführung eines neuen Behelfes an einer Stelle als nötig erwiesen, so muß man sich nun sofort fragen: Wo muß dieser Behelf nun immer angewandt werden? Seine Stellung in der Logik muß nun erklärt werden.

5.453

Alle Zahlen der Logik müssen sich rechtfertigen lassen.

Oder vielmehr: Es muß sich herausstellen, daß es in der Logik keine Zahlen gibt.

Es gibt keine ausgezeichneten Zahlen.

5.454

In der Logik gibt es kein Nebeneinander, kann es keine Klassifikation geben.

In der Logik kann es nicht Allgemeineres und Spezielleres geben.