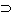 , etc., nicht Beziehungen im Sinne
von rechts und links etc. sind, leuchtet ein.
, etc., nicht Beziehungen im Sinne
von rechts und links etc. sind, leuchtet ein.
Die Möglichkeit des kreuzweisen Definierens der logischen "Urzeichen" Freges und Russells zeigt schon, daß dies keine Urzeichen sind, und schon erst recht, daß sie keine Relationen bezeichnen.
Und es ist offenbar, daß das "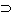 ", welches
wir durch "~" and "v" definieren, identisch ist mit dem, durch welches
wir "v" mit "~" definieren und daß diese "v" mit dem ersten identisch ist.
U.s.w.
", welches
wir durch "~" and "v" definieren, identisch ist mit dem, durch welches
wir "v" mit "~" definieren und daß diese "v" mit dem ersten identisch ist.
U.s.w.
Alle Sätze der Logik sagen aber dasselbe. Nämlich Nichts.
Wenn man z.B. eine Bejahung durch doppelte Verneinung erzeugen kann, ist dann die Verneinung -- in irgend einem Sinn -- in der Bejahung enthalten? Verneint "~~p" ~p, oder bejaht es p; oder beides?
Der Satz "~~p" handelt nicht von der Verneinung wie von einem Gegenstand; wohl aber ist die Möglichkeit der Verneinung in der Bejahung bereits präjudiziert.
Und gäbe es einen Gegenstand, der "~" hieße, so müßte "~~p" etwas anderes sagen als "p". Denn der Satz würde dann eben von ~ handeln, der andere nicht.
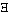 x) . fx", etc. sind,
sondern die allgemeinste Form ihrer Kombinationen.
x) . fx", etc. sind,
sondern die allgemeinste Form ihrer Kombinationen.
Sind ja schon im Elementarsatze all logischen Operationen enthalten.
Denn "fa" sagt dasselbe wie
"(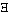 x) . fx . x=a".
x) . fx . x=a".
Wo Zusammengesetztheit ist, da ist Argument und Funktion, und wo diese sind, sind bereits alle logischen Konstanten.
Man könnte sagen: Die Eine logische Konstante ist das, was alle Sätze, ihrer Natur nach, mit einander gemein haben.
Das aber ist die allgemeine Satzform.