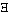HOME TOP UP PREV NEXT ENGLISH MAP      Logisch-philosophische Abhandlung 5.451

5.451

Hat die Logik Grundbegriffe, so müssen sie von einander unabhängig sein. Ist ein Grundbegriff eingeführt, so muß er in allen Verbindungen eingeführt sein, worin er überhaupt vorkommt. Man kann ihn also nicht zuerst für eine Verbindung, dann noch einmal für eine andere einführen. Z.B.: Ist die Verneinung eingeführt, so müssen wir sie jetzt in Sätzen von der Form "~p" ebenso verstehen, wie in Sätzen wie "~(p v q)", "(x) . ~fx" u.a. Wir dürfen sie nicht erst für die eine Klasse von Fällen, dann für die andere einführen, denn es bliebe dann zweifelhaft, ob ihre Bedeutung in beiden Fällen die gleiche wäre und es wäre kein Grund vorhanden, in beiden Fällen dieselbe Art der Zeichenverbindung zu benützen.

(Kurz, für die Einführung der Urzeichen gilt, mutatis mutandis, dasselbe, was Frege ("Grundgesetze der Arithmetik") für die Einführung von Zeichen durch Definitionen gesagt hat.)

HOME TOP UP PREV NEXT ENGLISH MAP      Logisch-philosophische Abhandlung 5.451