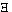HOME TOP UP PREV NEXT 1 2 3 4 GERMAN MAP      Tractatus Logico-Philosophicus 5.45

5.45

If there are logical primitive signs a correct logic must make clear their position relative to one another and justify their existence. The construction of logic out of its primitive signs must become clear.

5.451

If logic has primitive ideas these must be independent of one another. If a primitive idea is introduced it must be introduced in all contexts in which it occurs at all. One cannot therefore introduce it for one context and then again for another. For example, if denial is introduced, we must understand it in propositions of the form "~p", just as in propositions like "~(p v q)", "(x) . ~fx" and others. We may not first introduce it for oone class of cases and then for another, for it would then remain doubtful whether its meaning in the two cases was the same, and there would be no reason to use the same way of symbolizing in the two cases.

(In short, what Frege ("Grundgesetze der Arithmetik") has said about the introduction of signs by definitions holds, mutatis mutandis, for the introduction of primitive signs also.)

5.452

The introduction of a new expedient in the symbolism of logic must always be an event full of consequences. No new symbol may be introduced in logic in brackets or in the margin -- with, so to speak, an entirely innocent face.

(Thus in the "Principia Mathematica" of Russell and Whitehead there occur definitions and primitive propositions in words. Why suddenly words here? This would need a justification. There was none, and can be none for the process is actually not allowed.)

But if the introduction of a new expedient has proved necessary in one place, we must immediately ask: Where is this expedient always to be used? Its position in logic must be made clear.

5.453

All numbers in logic must be capable of justification.

Or rather it must become plain that there are no numbers in logic.

There are no pre-eminent numbers.

5.454

In logic there is no side by side, there can be no classification.

In logic there cannot be a more general and a more special.