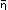HOME TOP UP PREV NEXT 0 1 2 3 ENGLISH MAP      Logisch-philosophische Abhandlung 6.0

6.0

6.00

6.01

Die allgemeine Form der Operation ' () ist also:
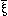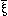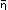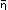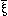[, N ()]'() (= [, , N()]).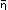

Das ist die allgemeinste Form des Überganges von einem Satz zum anderen.

6.02

Und so kommen wir zu den Zahlen: Ich definiere
x = ⁰'x Def. und
'^v'x = ^v+1'x Def.

Nach diesen Zeichenregeln schreiben wir also die Reihe x, 'x, ''x, '''x . . . . . so: ⁰'x, ⁰⁺¹'x, ⁰⁺¹⁺¹'x, ^0+1+1+1'x . . . . .

Also schreibe ich statt "[x, , ' ]",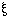

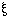"[⁰, ^v'x, ^v+1'x]",

Und definiere:

0 + 1 = 1 Def.
0 + 1 + 1 = 2 Def.
0 + 1 + 1 + 1 = 3 Def.
(u.s.f.)

6.03

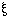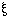Die allgemeine Form der ganzen Zahl ist: [0, , +1].