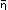HOME TOP UP PREV NEXT 0 1 2 3 GERMAN MAP      Tractatus Logico-Philosophicus 6.0

6.0

6.00

6.01

The general form of the operation ' () is therefore:
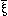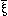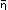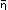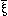[, N ()]'() (= [, , N()]).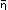

This is the most general form of transition from one proposition to another.

6.02

And thus we come to numbers: I define
x = ⁰'x Def. and
'^v'x = ^v+1'x Def.

According, then, to these symbolic rules we write the series x, 'x, ''x, '''x . . . . . as: ⁰'x, ⁰⁺¹'x, ⁰⁺¹⁺¹'x, ^0+1+1+1'x . . . . .

Therefore I write in place of "[x, , ' ]",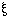

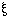"[⁰, ^v'x, ^v+1'x]",

And I define:

0 + 1 = 1 Def.
0 + 1 + 1 = 2 Def.
0 + 1 + 1 + 1 = 3 Def.
and so on.

6.03

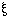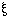The general form of the cardinal number is: [0, , +1].