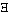 x, y) . f(x, y) . x=y",
sondern
"(
x, y) . f(x, y) . x=y",
sondern
"(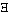 x) . f(x, x)"; und nicht
"(
x) . f(x, x)"; und nicht
"(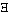 x, y) . f(x, y) . ~x=y",
sondern
"(
x, y) . f(x, y) . ~x=y",
sondern
"(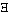 x, y) . f(x, y)".
x, y) . f(x, y)".
(Also statt des Russell'schen
"(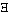 x, y) . f(x, y)" :
"(
x, y) . f(x, y)" :
"(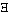 x, y) . f(x, y) .v.
(
x, y) . f(x, y) .v.
(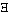 x) . f(x, x)".)
x) . f(x, x)".)
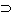 a=c",
"(x) . x=x".
"(
a=c",
"(x) . x=x".
"(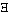 x) . x=a",
etc. sich in einer richtigen Begriffschrift gar nicht hinschreiben lassen.
x) . x=a",
etc. sich in einer richtigen Begriffschrift gar nicht hinschreiben lassen.
Alle Probleme, die Russell's "Axiom of Infinity" mit sich bringt, sind schon hier zu lösen.
Das, was das Axiom of Infinity sagen soll, würde sich in der Sprache dadurch ausdrücken, daß es unendlich viele Namen mit verschiedener Bedeutung gäbe.