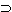 . x=a". What this
proposition says is simply that only a satisfies
the function f, and not that only such things satisfy the
function f which have a certain relation to a.
. x=a". What this
proposition says is simply that only a satisfies
the function f, and not that only such things satisfy the
function f which have a certain relation to a.
One could of course say that in fact only a has this relation to a, but in order to express this we should need the sign of identity itself.