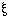 has only one value, then
N(
has only one value, then
N(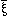 )=~p (not p), if it has two
values then N(
)=~p (not p), if it has two
values then N(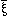 )=~p . ~q (neither
p nor q).
)=~p . ~q (neither
p nor q).
HOME TOP UP PREV NEXT 1 2 3 4 5 GERMAN MAP Tractatus Logico-Philosophicus 5.51
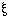 has only one value, then
N(
has only one value, then
N(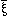 )=~p (not p), if it has two
values then N(
)=~p (not p), if it has two
values then N(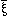 )=~p . ~q (neither
p nor q).
)=~p . ~q (neither
p nor q).
That which denies in "~p" is however not "~", but that which all signs of this notation, which deny p, have in common.
Hence the common rule according to which "~p", "~~~p", "~p v ~p", "~p . ~p", etc. etc. (to infinity) are constructed. And this which is common to them all mirrors denial.
And similarly we can say: Two p ropositions are opposed to one another when they have nothing in common with one another; and every proposition has only one negative, because there is only one proposition which lies altogether outside it.
Thus in Russell's notation also it appears evident that "q : p v ~p" says the same thing as "q"; that "p v ~p" says nothing.
And this is the case, for the symbols "p" and "q" presuppose "v", "~", etc. If the sign "p" in "p v q" does not stand for a complex sign, then by itself it cannot have sense; but then also the signs "p v p", "p. p", etc. which have the same sense as "p" have no sense. If, however, "p v p" has no sense, then also "p v q" can have no sense.