HOME TOP UP PREV NEXT 1 2 3 4 GERMAN MAP      Tractatus Logico-Philosophicus 4.127

4.127

The propositional variable signifies the formal concept, and its values signify the objects which fall under this concept.

4.1271

Every variable is the sign of a formal concept.

For every variable presents a constant form, which all its values possess, and which can be conceived as a formal property of these values.

4.1272

So the variable name "x" is the proper sign of the pseudo-concept object.

Wherever the word "object" ("thing", "entity", etc.) is rightly used, it is expressed in logical symbolism by the variable name.

For example in the proposition "there are two objects which . . .", by "(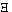x, y) . . .".

Wherever it is used otherwise, i.e. as a proper concept word, there arise senseless pseudo-propositions.

So one cannot, e.g. say "There are objects" as one says "There are books". Nor "There are 100 objects" or "There are ₀ objects".

And it is senseless to speak of the number of all objects.

The same holds of the words "Complex", "Fact", "Function", "Number", etc.

They all signify formal concepts and are presented in logical symbolism by variables, not by functions or classes (as Frege and Russell thought).

Expressions like "1 is a number", "there is only one number nought", and all like them are senseless.

(It is as senseless to say, "there is only one 1" as it would be to say: 2 + 2 is at 3 o'clock equal to 4.)

4.1273

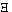If we want to express in logical symbolism the general proposition "b is a successor of a" we need for this an expression for the general term of the formal series: aRb, (x) : aRx . xRb, (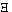x, y) : aRx . xRy . yRb, . . . The general term of a formal series can only be expressed by a variable, for the concept symbolized by "term of this formal series" is a formal concept. (This Frege and Russell overlooked; the way in which they express general propositions like the above is, therefore, false; it contains a vicious circle.)

We can determine the general term of the formal series by giving its first term and the general form of the operation, which generates the following term out of the preceding proposition.

4.1274

The question about the existence of a formal concept is senseless. For no proposition can answer such a question.

(For example, one cannot ask: "Are there unanalysable subject-predicate propositions?")