Nehmen wir nämlich an, die Funktion F(fx) könnte ihr eigenes
Argument sein; dann gäbe es also einen Satz "F(F(fx))"
und in diesem müssen die äußere Funktion F und die innere Funktion
F verschiedene Bedeutungen haben, denn die innere hat die Form
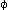 (fx),
die äußere, die Form
(fx),
die äußere, die Form
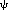 (
(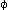 (fx)).
Gemeinsam ist den beiden Funktionen nur der Buchstabe "F", der aber
allein nichts bezeichnet.
(fx)).
Gemeinsam ist den beiden Funktionen nur der Buchstabe "F", der aber
allein nichts bezeichnet.
Dies wird sofort klar, wenn wir statt "F(F(u))"
schreiben
"(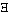
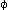 ) : F(
) : F(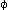 u) .
u) . 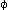 u=Fu".
u=Fu".
Hiermit erledigt sich Russell's Paradox.